ヘリコプタもドローンも、鉛直方向の軸を持つプロペラで下向きの流れを作り、その反力を浮上に利用します。プロペラ回転面を進みたい方向にわずかに傾け、反力の水平方向成分を水平移動の推力として利用します。プロペラ面を傾ける方法が両者で異なります。
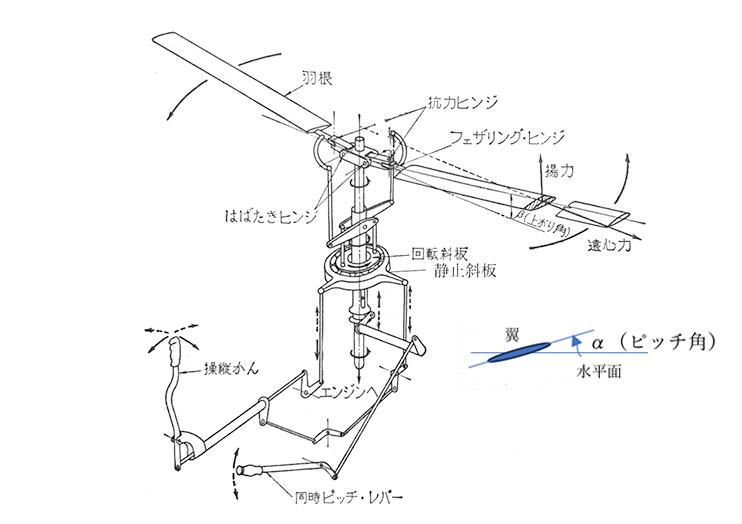
図1 ヘリコプタのプロペラ(1)
機体の運動制御を考えます。図1中の回転斜板は、操縦桿の操作方向に傾けられた外側の静止斜板に接しながら軸とともに回転し、回転斜板につながるリンク機構によって翼取り付け角(翼前縁と後縁を結ぶ方向と水平面のあいだの角度、ピッチ角α、図1参照)をフェザリングヒンジを軸として1回転に1回変動させ(サイクリックピッチコントロール)、これによってプロペラ回転面を操縦桿を傾けた方向に傾け、機体の水平方向の運動を制御します。実機のサイクリックピッチコントロールとこれに基づくはばたき運動の例です:
https://www.youtube.com/watch?v=X2BWvdnWmno
同時ピッチレバーによって回転斜板は上下に平行移動し、平均ピッチを変えて機体の上昇・下降を制御します。回転斜板と静止斜板を組み合わせた機構をスウオッシュプレートと呼びます。回転斜板と静止斜板の軸方向位置と傾斜角度は同一となりますが、それらの間にベアリングが置かれ回転斜板は軸とともに回転します。静止斜板の軸方向位置と傾斜角度は機体側からリンク機構によって操作され、回転斜板はこれと同じ位置と角度となって回転翼のピッチ角を制御します。
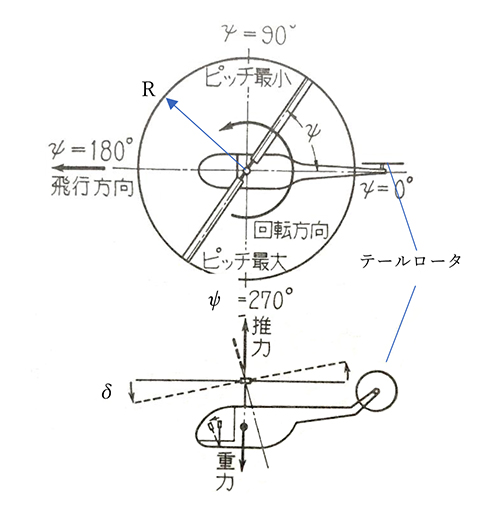
図2 機体が前進するときの周期的ピッチ制御と回転面傾斜(1)
周期的ピッチ制御によってプロペラ回転面が角度δ<<1(rad)だけ前方に傾いた場合を考えます。プロペラ回転角ψ、半径Rの位置における傾斜回転面の高さzを水平面から測ると次のようになります。


式(2)の第1項と第2項の間の等式は設定したピッチ角 α*とプロペラ軌道の勾配が一致するとする条件式です。第2項と第3項の間の等式はピッチ角を右辺のように具体的に与えるもので、これを積分することによって式(1)が得られ、式(1)はプロペラ回転面が進行方向にδだけ傾いた平面であることを表しています。すなわち、翼がピッチ角の方向に進むことを仮定すれば、式(2)のピッチ角制御によって回転面はδだけ傾くことを表しています。ここでは翼の慣性が流体力に対して無視でき、また流体力は翼に対する相対流れ角に比例するものと仮定しています。
翼が水平回転面内で回転し、ピッチ角が式(2)に従って変動するものとします。揚力がピッチ角に比例するものと考えると0°<ψ<180°では下向きの揚力、180°<ψ<360°では上向きの揚力が作用し、プロペラ回転面には進行方向ψ=180°に向かって時計方向のモーメントが作用します。その結果として最終的にプロペラ回転面が前方にδだけ傾き、回転面の角変位はψ=270°方向を向きます。角変位の方向とモーメントの方向が90°ずれることは、回転体の角運動量ベクトルの変化とその原因となるジャイロモーメントの関係、“ジャイロ効果”、と定性的に一致します。(注:ジャイロ効果は、“質点群に作用する外力モーメント=質点群の持つ角運動量の時間変化率”とする角運動量保存則から説明されますが、ここでの議論は作用する流体力モーメントの方向と角運動量の方向変化の関係が角運動量保存則と矛盾しないことを定性的に論じたものです。定量的に運動を論じるには角運動量保存則を適用する必要があります。ジャイロ効果は、コマの歳差運動を説明します。)
次に傾斜回転面内のプロペラの運動を考えます。前述のようにこの面内での翼面の方向は移動方向と同一であると仮定しているので、プロペラ面に流体力は作用せず、プロペラはこの傾斜回転面内を回り続けます。水平回転面内の運動を保ったままピッチ角変動を加えると、ピッチ角変動による揚力変動が現れ、これによって翼にはばたき運動が生じた結果回転面に傾斜が生じることになります。図3に、周期的ピッチ制御を行った場合の翼の動きを、式(1)の自由なはばたき運動を許した場合と、翼の運動を水平面内に拘束し式(2)のピッチ角変動を与えた場合について示します。はばたきを許した場合には流体力は発生せず、水平面内に拘束した場合にはピッチ角に比例した揚力変動が発生します。
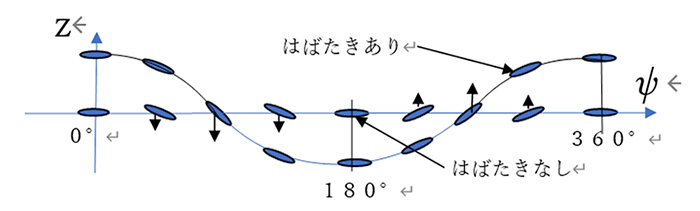
図3 周期的ピッチ制御による翼の動き

操縦桿を前に倒し式(3)のピッチ角変動をあたえると、プロペラ回転面は前進方向に傾き始め、傾斜角はδに漸近します。回転面に作用する全揚力はψ=180°の方向にδだけ傾いてその前進方向成分として前進推力が得られます。同様に操縦桿を左右に倒すと回転面も左右に傾き、左右方向の推力成分が得られます。
プロペラ回転面の角変位は機体から回転軸を介して回転面に加えられるモーメントではなく、プロペラに作用する空気力の変化によって実現されています。
横滑りに対する安定性およびオートローテーション
次に、図2の前進の場合でピッチ角が一定に保たれた場合を考えます。ψ=0°~180°では機体の前進により翼と空気の間の相対速度並びに揚力が大きくなり、ψ=180°~360°では相対速度並びに揚力が小さくなるので回転面には進行方向に向かって反時計回りのモーメントが作用します。このモーメントは周期的ピッチ変動を考えた場合と逆方向なので、プロペラ回転面並びに全揚力はジャイロ効果によって図2に示した方向とは逆に後方、ψ=0°の方向に傾き、機体を減速させることになります。このように、ピッチを一定に保ったまま横方向に移動すると、移動速度と反対方向の力が現れます。つまり、仮に横滑りがあった場合にはその滑りを止める復元力が現れることになるので、横滑りに対して静的には安定であることを示します。
以上のようにヘリコプタでは揚力並びに推力を得るために複雑な機構と制御が必要です。ここで議論したようにホバリング時は横滑りに対して復元力が働いて静的には安定ですが、より詳しい議論をすれば動的には不安定であるので高度な操縦技術が要求されます。しかしながらドローンのような小型機でなく大型の機体では不安定の周期は長いので、パイロットの制御によって安定に飛行させることが可能となります。
エンジンが故障した場合にはエンジンとプロペラを切り離したうえで負のピッチ角を与えることでプロペラは風車のように回転を続け、機体は滑空することができます。これはオートローテーションと呼ばれる安全上重要な機能です。
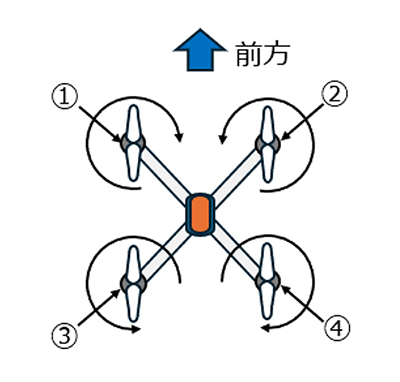
図4 ドローン(クアドコプタ)
このとき、
- ①と②、③と④のプロペラの反モーメントはそれぞれ相殺するのでテールロータは不要である。
- 前進させるためには①と②の回転数を減少させ、③と④の回転数を同じだけ増加させる。この回転数変化によって機体姿勢は①と②が下がり、③と④が上がる方向に傾き、前向きの推力が発生する。①と②、また③と④の反モーメント並びにジャイロモーメントはそれぞれ相殺し、姿勢変化に影響しない。但し、各プロペラには機体から軸を介して反モーメント並びにジャイロモーメントが作用する。プロペラの推力は翼根の曲げモーメントで支持されている。前進速度によってプロペラに作用する揚力が変動し、機体を励振する。プロペラおよび軸はこれらの力に耐える強度を持たねばならない。
- 後退、右方向、左方向移動の場合も、移動方向に“前進”するものと考えて同様の操作をすればよい。
- 機体を水平面内で時計方向に回転させるためには、時計方向回転のプロペラ①と④の回転数を減少させ、反時計方向回転のプロペラ②と③の回転数を同じだけ増加させればよい。
- 上昇・降下させるには、すべてのプロペラの回転数を同じだけ増加・減少させればよい。
ドローン操縦士は基本的に
(1)前後方向移動速度
(2)左右方向移動速度
(3)水平面内回転角速度
(4)上昇・降下速度
など、機体の速度変化を指示することになりますが、これはヘリコプタの操縦で直接操作するのは機体の運動ではなくスウオッシュプレート位置と傾きすなわちプロペラのピッチ角であることと大きく異なります。これらの操作情報は送信機から受信機に送られます。受信機ではこれらの情報をフライトコントローラに送り、フライトコントローラはこれを実現すべく4台のモータの回転数を前節で述べたようにコントロールします。ヘリコプタ操縦士には操作に対する機体の応答を予測する能力が求められますが、ドローンではフライトコントローラが以下に述べるように機体の応答信号を用いてフィードバックを加えることで機体の運動自体を制御してくれるので操縦が容易となり、これがドローン普及の一因となっています。
フライトコントローラには
(1)ジャイロ・加速度センサから姿勢・加速度に関する情報
(2)気圧センサあるいは超音波距離センサによる高度に関する情報
が送られ、風などの外乱があっても要求動作が実現されるよう各モータの回転数が制御されます。 機体の姿勢や運動など複数の制御値を同時に目標値に近づけるために、状態フィードバック制御という現代制御の手法を用いて4つの回転翼の回転数が決定されています。
特定のプロペラの空力性能が悪くても、必要な揚力が得られるまで回転数を増加させるため飛行は可能です。ヘリコプタの操作はスウオッシュプレートの位置および傾きとして非運転時にも直接確認できますが、ドローンの操作に対する運動応答は非運転時には直接確認できないのが難点です。
このほか、ドローンでは
(3)GPSによる位置検知
(4)磁気方位センサによる方位の検知
が行われ、定点ホバリング、自動帰還、自動着陸、自動運行なども可能です。ヘリコプタにもフライトコントローラを装備すればドローンと同様の操縦性を実現することも原理的には可能です(https://www.youtube.com/watch?v=twYYlgnYavQ)。
ドローンが実用化されたのは有用な用途が現れたことが一番大きな理由ですが、これが実現できたのは制御プログラムが開発されたのに加えて
(2)小型高効率同期モータ
(3)MEMSを用いた超小型高感度ジャイロ・加速度センサ、圧力計
(4)小型GPS並びに磁気方位センサ
が低コストで利用できるようになり、
(5)周波数ホッピングやダイバーシテイアンテナ
により無線通信の信頼性向上があったためです。
(1) 各要素の信頼性向上と安全性の確保
(2) 稼働範囲拡大に伴う動力源の大容量化とエネルギ効率向上
(3) 大型化に伴うプロペラ・軸系の強度の確保と振動・騒音対策
(4) 動力喪失時の滑空機能、あるいはこれを補填する機能の確保
(5) GPSが利用できない場合の位置検出法(慣性航法、画像認識など)の開発
交通への応用に関連して、騒音低減、大容量動力源、ハイブリッド化、モーターの効率化などについての特集記事が「ターボ機械協会誌」に掲載されています(3)。
ドローンは小型で単純な機構が最も大きな利点です。大型化はこれに反するものなので、この利点を損なわないことを念頭に適用範囲の拡大を図る必要があります。
謝辞:本稿の準備には宮本洋氏、姜東赫氏の貴重なご助言をいただいたので深く感謝します。
- 航空宇宙工学概論再訂版、三木鉄夫編、森北出版、1979.
- トコトンやさしいドローンの本、鈴木真二監修、日刊工業新聞社、2016.
- 特集:アーバンエアモビリテイとターボ機械、ターボ機械、御法川学編、2024-11,
「ドローン(Drone)」と言う術語は,元々は,アメリカ海軍少佐Delmer S. Fahrneyが,英国の標的航空機DH.82クイーンビー(DH.82 Queen Bee)に敬意を表して,自分達米海軍が開発する無人航空機(Unmanned Aerial Vehicle, UAV)の事を雄蜂に例えて作り出したコードネームでした([HP1][HP2]を「coined(新語を作る)」で検索).そして,2010年にフランスParrot社が「AR Drone」を発売した事で広く一般に認知される様になり,様々なドローンビジネスが考案される様になりました.
しかし,現在では,無人地上機(Unmanned Ground Vehicle, UGV)は「地上ドローン」,無人潜水機(Unmanned Underwater Vehicle, UUV)は「水中ドローン」,無人水上機(Unmanned Surface Vehicle, USV)は「水上ドローン」等の様に,無人機(Uncrewed Vehicle/ Unmanned Vehicle,共にUV)の大半に対する通称として,「ドローン(Drone)」と言う術語が使用される様になっています.そこで,これらのドローンの因子をいくつか取り上げて考えてみましょう.
なお,現在「Drone」と言うと「マルチコプター(Multirotor)」を思い浮かべる事も多いと思います.「マルチコプター(Multirotor)」が「Drone」に分類される様になったのは,上記「AR Drone」の成功以降です.それ迄は,起源的理由から,「Drone」とは専ら軍事用自律機の事でした.この事は,例えば,「マルチコプターの歴史」や「Multirotor Notes」を見ると,「ドローン/Drone」と言う述語が使用されているのが2010年以降となっている事から分かります.そして,「AR Drone」の成功にあやかる為に,自律型UV全般(UGV/UUV/USV/等)で,「〜Drone」と言う呼称を使う様になって来たと言う訳です.
本稿では,ドローンの本質的機能と,それが必要とされた歴史,及び,これらに関連したエピソードなどについて,説明したいと思います.
2.ドローンの機能
2-1. ドローンと「無人」
ドローンの第一因子として「無人(Unmanned)」を考える人は多いと思います.しかし,「有人ドローン(Passenger Drone)」と言うものがあります.一方で,「空飛ぶ車(Flying Car)」もあります.何が違うのでしょうか?それは,前述の,uncrewedから分かる様に,「乗組員/乗務員/操縦士」が搭乗してないものがドローンです.つまり,Unmannedより,Uncrewedの方がより適切な術語であると言えます. 2-2. ドローンと「無人技術」
次に,「無人」を実現する技術「テレロボティクス(Telerobotics)」について考えてみます.これには大きく分けて,2つの技術,即ち,「遠隔制御(Remote Control, RC)」と「自律制御(Autonomous Cotrol)」があります.通例,ドローンと言えば,この「遠隔制御」をイメージすると思います.
前者の「遠隔制御(Remote Control, RC)」では,操縦者は搭乗していないだけで,操縦者は必要です.よって,「遠隔操作(Telecommand,TC)/遠隔操縦(Teleoperation)」/遠隔操作車両(Remote-Control Vehicle)」等,共呼ばれています.
一方,後者の「自律制御」は,「自律操縦(Autopilot)」「Pilotless」「自律システム(Autonomous System)」「自律ロボット(Autonomous Robot)」等,共呼ばれ,操縦者は必要ありません.上述の「有人ドローン(Passenger Drone)」は,目的地を告げる(入力する)だけで自律的に目的に到達するので,「自動操縦」です.現在開発されているドローン宅配用の「宅配ドローン(Delivery Drone)」は,完全自律化された場合でも,「宅配ドローン」と呼ばれるでしょう.
参)「自動運転車(Self-driving Car)/スマートカー(Vehicular Automation)」
ところで,乗客が乗っていても,操縦者が乗っていないものが「ドローン」なのであれば,「自動運転車(Self-driving Car)/スマートカー(Vehicular Automation)」も「ドローン」と呼んでも良さそうです.しかし,こちらも,通例ドローンとは呼ばれません.
2-3. ドローンと「遠隔技術」
ドローンと言えば,電気通信(Telecommunication)を利用した「遠隔制御」をイメージするでしょう.これにも2つの技術が存在します.「有線(Wired)」と「無線(Wireless)」です.ドローンと言えば「無線通信(Wireless Communication)」をイメージする事が多いと思います.しかし,有線ドローンには,24時間稼動可能/法的緩和/喪失防止/等の利点がある為,建築用/建設用/災害用/観測用/通信基地用/等の,様々な「有線通信(Wired Communication)」が考案/開発されています.
水中では,水分子が電波を急減衰させる為に,遠距離無線通信は困難です.そこで,無人潜水機(Unmanned Underwater Vehicle, UUV)は,有索式潜水機(Remotely Operated Underwater Vehicle, ROUV)か,自律型無人潜水機(Autonomous Underwater Vehicle, AUV)[HP]の2種類となっています.そして,前者を「水中ドローン」,後者を「水中ロボット」と呼ぶ事が多いですが,両方の無人潜水機を「水中ドローン」,或は,「水中ロボット」とする場合もあります.また,自動操縦無人潜水機にも,電力供給/有線通信/係留/喪失防止/等,操縦以外の目的で有索/有線である事もあります.
参)索
「索」とは,丈夫な,線(Cord)/ロープ(Rope)/ワイヤー(Wire)の事です.船を繋ぎ止める係留索,人を繋ぎ留める命綱等があります.
ここで,有線ドローンにおいて,電力/通信/推進剤/等の消耗品を供給する,ケーブル(Cable)/ホース(Hose)(を束ねたもの)を「アンビリカルケーブル(Umbilical Cable)」と呼びます.また,係留索/命綱を束ねる/兼ねるものもあります.
参)アンビリカルケーブル(Umbilical Cable)
「アンビリカツケーブル」とは,元々は,送気式潜水(Surface Supplied Diving)において「潜水服(Standard Diving Dress)」に使用する空気供給ホースが,母親が胎児へ栄養と酸素を送り込む「へその緒(Umbilical Cord)」を連想させる事から作られた造語でした.TVアニメ新世紀エヴァンゲリオンで有名になりました.なお,エヴァンゲリオンではアンビリカル・ブリッジと言う新造語も使われています.今では,潜水用だけでなく,無人潜水機用,ミサイル/ロケット発射台(Launch Pad),宇宙船外活動等様々な分野で,消耗品の供給ケーブル(の束)を「アンビリカル・ケーブル」と通称しています.下図では,宇宙飛行士が右手に持っている宇宙銃(Hand-Held Maneuvering Unit)へ窒素(推進剤)を供給する金色のアンビリカルケーブルと,白の命綱を使用しています.

図1.1. ジェミニ4号(Gemini 4)宇宙飛行士のアンビリカルケーブル
2-4. ドローンと「自動(Automation)」
ドローンには,「自動(Automation)」と言う特性があります.これは,前述の「自律(Autonomy)」よりやや緩い制御です.例えば,オートマチック(Automatic)車と言えば,自動変速機(Automatic Transmission, AT)付自動車の事ですが,自動運転車(Autonomous Car)と言えば,自律運転車(Self-Driving Car)を意味します.大雑把に言えば,「自動(Automation)」の大半は「半自動(Semi-Automation)」です.そして,人の介入を全く不要にしたものが「完全自動(Full Automatic)」の,更に上位の自動性が「自律(Autonomy)」です.
参)「自動(Automation)」
「自動人形/オードマトン(Automaton)」から派生した概念です.
古代ギリシャ語において,「autos=」は「自ら/自発の」,「matos=」は「動き=motion」を意味しますので,「自ら動く」と言う意味です.日本語では,複数形の「オートマタ(Automata)」も良く目にします.
参)「自律(Autonomy)」
勿論,「autos=」+「nomos=」で,nomos(ノモス)は「法律」です.よって,-は「自らを律するもの」と言う意味です.
参)「自律神経(Autonomic Nervous System)」
「自律神経(Autonomic Nervous System)」は,身体の恒常性(Homeostasis)を保つもので,ランニング時に心拍数/体温/発汗を制御する必要がありません.「倒立振り子(Inverted Pendulum)」と言う不安定状態にある「直立」と言う姿勢を維持出来るのも自律神経のおかげです.普通にしていると,自律性を認識出来ないのですが,何回か自転した後,或は,目を瞑って,直立してみると,直立姿勢を保てない事が分かります.前者は三半規管異常の為に,後者は視覚情報喪失の為に,自律神経が直立の安定を保てない例です.
参)半自動/完全自動/自律
半自動/完全自動には,対象物,或は,レベルがあります.例えば,変速機(Transmission)を考えます.変速は「クラッチを踏む→アクセル操作でエンジン回転数を合わせる→ギヤを上げる/下げる→クラッチを離す」と言う動作をします.この時,一般のAT車では,全てを自動化しているので「Full Automatic」と呼ばれます.一方,クラッチ作業のみを省略して「ギヤを上げる/下げる」のみ人が行なうものは「セミオートマチック(Semi-Automatic Transmission)」と呼ばれ,レーシングカーをはじめ,スポーツカー
同様に,銃にも「Semi-automatic/Full Automatic」がありますが,いずれも引き金を引くのは人なので,「自律(Autonomy)」とは言えません.一方,近接防空システム(CIWS)やミサイル(Missile)は「自律(Autonomy)」です.
この様に,「自律」「自動」にもレベルがあり,区別が難しい場合もありますので,これら2つを余り区別せずに使用している事も多くなっています.結果,ドローンにも,「自律」「半自動」「完全自動」等,様々なものが存在する事になります.
2-5. ドローンとラジコン(Radio-Controlled Model)
時々,「ドローンとラジコンは何が違うのですか?」と言う質問を受けます.そこで,ラジコンについて説明しましょう.
日本語の「ラジコン」は 増田屋コーポレーションの「おもちゃその他の区分」における登録商標です.結果として,趣味的なものはラジコン,実用/仕事に使われるものはドローンと呼ばれる事が多いと思います.
なお,「ラジコン」は,英語では「Radio-Controlled Model」です.略称は,RC(或はR/C).結果としてRCと言う表記は,「Radio Control」「Remote Control」「Radio-Controlled Model」のどれであるのか,曖昧な場合が時々見られます.
3.ニコラ・テスラ(Nikola Tesla)
3.1. テスラの無線通信
1887年に,ハインリヒ・ヘルツ(Heinrich Hertz)が,電磁波を生成/検出する機械を開発する事によって,その存在を証明(Annalen der Physik, vol.267, pp.421-448(1887))して以来,電磁波(Electromagnetic Radiation),特に,電波(Radio Wave)を用いた無線伝送(Wireless Transmission)への関心が高まりました.
テスラは,1891年5月20日のニューヨーク市コロンビア大学での講演を皮切りに,1893 年 2 月 24 日にはフィラデルフィアのFranklin Instituteで,同年3月1日にはセントルイスのNational Electric Light Associationで,無線電力伝送(Wireless Power Transfer)/無線通信(Wireless Communication)/無線電信(Wireless Telegraphy)に関する一連の講義とデモを行ないました.また,それはNature誌上(Nature, 48, pp.136–140 (1893))でも発表されています.これらは,1895年のグリエルモ・マルコーニ(Guglielmo Marconi)の無線通信成功に先立つ2年前でした.
3.2. テスラの無人無線機(Teleautomaton/Telautomaton)
さて,1898年5月6日,テスラは,Madison Square Gardenで,下図の様なボート模型の実演を行ないました[HP].これは後に「Teleautomaton/Telautomaton」と呼ばれる様になりました.このTeleautomatonは,世界初のドローン(正確には水上ドローン)です.この遠隔無線技術は,同年7月1日に申請され,同年11月8日に承認された「US Patent No.613809」としても有名です.
参)Teleautomaton
前述の様に,ギリシャ語において,「automaton=」は「自動人形/オートマトン」),また「tele=」は「遠隔」なので,Teleautomatonは,「遠隔自動機」「遠隔ロボット」と言う意味になります.これにより,テスラは「Father of Robotics」共呼ばれています.
参)電波(Radio Wave)
電磁波(Electromagnetic Wave)のうち,周波数10 kHz〜3 THz(波長0.1 mm〜3 km)のもので,「高周波/無線周波数(High Frequency /Radio Frequency)」等共呼ばれます.なお,可視光は,周波数400〜800THz(波長400〜800nm)です.
なお,テスラはX線を発見し,X線写真の事を「Shadow Graph」と呼びました.この呼称は,流体力学でもシャドーグラフ法として登場します.しかし,1895年3月13日のNY研究所の火事で全てを失いました.また,彼は,ある種の勘違いとは言え,X線の有害性を認識していましたし,防護方法も考案していました.
その後,1895年11月8日に,ヴィルヘルム・レントゲンによってX線の発見が発表されると,テスラは,手元に残っていたX線写真をレントゲンに送りました.レントゲンはそのクリアな画像に驚嘆し,「どの様にすればその様な写真が撮影できるのか」と質問しました.
参)AND回路
Teleautomatonでは,後に「US Patent No. 725,605」として申請される事になる,人類初の論理回路(Logic Gate)である「ANDゲート(AND Logic Gate)」が搭載されていました.
参)TDSのラジコン船
皆さんの中には,東京ディズニーシーのフォートレス・エクスプロレーション中のナビゲーションセンターにあるラジコン船を操作した事がある人もいると思います.上図を見て貰えば,「あれは,Teleautomatonなのではないか?」と考えると思います.もしかしたらTDSのラジコン船のモチーフは,このテスラのTeleautomatonなのかも知れません.
3.3. テスラの無線魚雷(Wireless Torpedo)
テスラはTeleautomatonを「無線魚雷(Wireless Torpedo)」として,米海軍に売り込みました(「私の潜水艦駆逐艦(My Submarine Destroyer)」).現在なら,Teleautomatonに爆弾を積んで敵艦に突撃させれば「対艦兵器/対艦ミサイル(Anti-Ship Missile)」になると分かります.実際,Teleautomatonはミサイルの起源と見做されています.しかし当時の米海軍はその革新性に気づく事が出来ませんでした.
参)魚雷(Torpedo)
日本語の「魚雷」は,「魚形水雷」略称です.一方,英語のTorpedoは,シビレエイ目(Electric Ray)目Torpedo属が起源の呼称です.ラテン語Torpedo/英語Tordedo共に,「固まる/硬直する/麻痺する」と言う意味です.
参)テスラの世界システム(World System)
軍の興味を引く事が出来なかったテスラは,ドローンから離れ,彼は高電圧変圧器テスラコイル(Tesla Coil)を用いた「World System/World Wireless System」により世界の人・物・情報・エネルギーが繋がる未来を目指しました.
世界システムは,ウォーデンクリフ・タワー(Wardenclyffe Tower/Tesla Tower)をハブとした世界無線システムでした.今ならその革新が理解出来ますが,当時は空想と見做されました(実際,失敗しました).図を見ると,テスラの構想が一目瞭然です.また,現在の無線を使用した技術の多くが図に記載されており,テスラの発想の革新性を理解する事が出来ます.「World System」を考える時,ジュール・ヴェルヌの「Tout ce qu'un homme est capable d'imaginer, d'autres hommes seront capables.(想像出来るなら実現出来る)」や,ウォルト・ディズニーの「If you can dream it, you can do it.(夢見る事が出来るなら実現出来る)」を思い出します.
4. レオナルド・ケベード(Leonardo Quevedo)のテレキノ(Telekino)
1901年,ケベードは,自身の飛行船の開発試験を安全に実施する為に,飛行船を無人化しようと考え,「テレキノ(Telekino)/テレキネ(Telekine)」(κίνησις=kinesis=運動)と呼ばれる無線装置の開発を開始しました.そして,1904年に三輪車をTelekinoで動かしました.これは,人類初のUGVだと思います.また,1905年にラジコン船も動かしています.
5.飛行爆弾(Flying Bomb)
1783年6月4日,モンゴルフィエ兄弟が熱気球の公開飛行を,また1783年8月27日にはロベール兄弟が水素気球の公開飛行を,それぞれ実施しました.但し,これらは,紙飛行機の様なものであり,無人航空機(Unmanned Aerial Vehicle)とは呼べません.輸送機(Vehicle)としては,1783年9月19日,これまた,モンゴルフィエ兄弟が,ベルサイユ宮殿前広場で,ルイ16世とマリーアントワネットの眼前で,「レヴェイヨン気球(Aérostat Réveillon)」に動物を乗せて無人飛行を成功させたのが,世界初の無人航空機(Unmanned Aerial Vehicle)と言えます.そして,これ以来.気球や飛行船は,偵察や射弾観測,空襲等への利用が考えられて来ました.1849年,オーストリア海軍は, 気球母艦(Balloon Carrier)ヴルカノ(Vulcano)を用いて,人類初めて,熱気球でイタリアのヴェニスを空爆しました.熱気球は航空機であり,また,この熱気球爆弾は無人だったので,これは,世界最初のUAVの実用例です.この様な航空兵器(Aircraft Weapons)に対抗する為に, 対空兵器(Anti-aircraft warfare)が開発されました.
1896年,アルフレッド・ノーベルは,カメラを搭載したロケットの特許を申請しました.ノーベルの死後,1897年になってから,ロケットが打ち上げられ,世界初の航空写真の撮影が行われました.
そして,1903年のライト兄弟が人類初の動力飛行に成功すると,地対空兵器(対空砲)の一種として「飛行爆弾(Flying Bomb)」と言うアイデアが生まれました.飛行爆弾とは,無人飛行機に爆弾を積んで,遠隔で,或は,自動で,飛行船を追跡して撃ち落とすUAVで,対空兵器としてだけでなく,対艦兵器/対地兵器としても有用である事は言うまでもありません.このアイデアはやがて,V1飛行爆弾やミサイル(Missile)/巡航ミサイル(Cruise Missile)に繋がる事になります.それ故,飛行爆弾は巡航ミサイルの起源と言われています.
類似のものに「誘導爆弾(Guided Bomb)」がありますが,こちらは航空機から放たれるもの(通例,推進機を持たないもの)を言います.最初期の誘導爆弾で有名なのは,ジーメンス(Siemens)が開発した,「滑空魚雷(Torpedo Glider)」です.但し,これは無線ではなく有線でした.
なお,2022年2月24日に始まったウクライナ戦争におけるドローンの運用方法(Drone Warfare)は,このドローンの起源である,対空/対艦/対地兵器としての「飛行爆弾」に回帰していると言えます.
参)航空魚雷(Aerial Torpedo)
飛行爆弾は,米海軍では,航空魚雷(Aerial Torpedo)と呼ばれました.但し,航空魚雷は,厳密に言えば,対空兵器ではなく,対艦兵器/対艦ミサイル(Anti-Ship Missile)です.また,現在,航空魚雷と言えば,「雷撃機(Torpedo Bomber)」から投下するものをイメージすると思います.なお,世界初の雷撃は,1915年8月12日の「ショート 184(Short Type 184)」によるものですので,前述のテスラのWireless Torpedoと言うアイデアが時代を15年先取りしていた事が分かります.
参)「The Airship Destroyer(1906)」
1906年に公開されたSF映画です.原題は「Der Luftkrieg Der Zukunft」で,「Luft=空,Krieg=war,Zu=to,kunft=come(或は,Zukunft=未来)」なので,直訳すれば「the aerial war to come=未来の空中戦争」となります.ところが英国題は「The Aerial Torpedo(YouTube)」でした.何故この様な題名にしたのでしょうか?その理由は,ストーリーにあります.ストーリーを大雑把に言えば「未知の飛行船艦隊が襲来し街を空爆します.町側は飛行機からの砲撃で撃墜を試みますが歯が立ちません.最後に飛行爆弾を発射して迎撃に成功する」と言うものです.この様に,劇中で飛行爆弾が使用されたので,「The Aerial Torpedo」と言う題名になった訳です.ここで使用された飛行爆弾は,飛行機型無線操縦の地対空ミサイルでした.ドイツのツェッペリン号による世界爆撃は,1914年8月の第1次世界大戦における爆撃ですから,これに先んじる事5年前(構想はもっと前でしょう)の予言的映画で,1915年に再上映されました.類似の映画に,米国の「The Flying Torpedo(1916)」があります.
6.世界初の自動操縦機
サミュエル・ラングレー(Samuel Langley)は,エアロドローム(Aerodome)と呼ばれる無人自動操縦模型機を開発しました.そして,1896年5月6日,彼は「エアロドローム5」の飛行に成功しました(このエアロドローム5の再現映像がYouTubeで公開されています).なお,ギリシャ語「aer」は「空気/空中」を,dromosは「道/走るもの」を意味するので,Aerodromeとは「空中を走るもの」と言う意味です.「エアロドローム5」は,人類初の無人の自動操縦機でした.エアロドームは「航空爆弾」として利用可能と考えられますが,残念な事に,「航空爆弾」と言うアイデアに繋げる事は出来ませんでした.
1910年,Elmer Sperryは,自ら発明した実用ジャイロスコープ(Gyroscope)であるジャイロコンパス(Gyro-Compass for Battleship/Gyro-Stabilizer for Destroyer)を製造販売する為に, スペリー社 (Sperry Gyroscope Corporation)を設立しました.そして,Gyroscope Autopilotを1912年に開発しました.また,彼の三男Lawrence Sperryは,これを改良し,グレン・カーチス(Glenn Curtiss)が設計し,Curtiss Aeroplane and Motor Company製が製造したCurtiss C-2(Curtiss Model Fの海軍コード番号)にGyroscopic Stabilizerを搭載し,1914年6 月 18 日に,フランスの飛行機安全競技会において自動で離陸/飛行/着陸を行いました.これが人類初の有人自動操縦機です.
7.米国における飛行爆弾
1917年9月,Peter HewittとElmer Sperryは,米海軍用に,Curtiss N-9にスペリー社製Gyro-Stabilizerを搭載して,開発した「Hewitt-Sperry Automatic Airplane/ Curtiss-Sperry Flying Bomb」の初飛行試験を成功させました[YouTube 2:03].
また,1918年10月2日,チャールズ・ケタリング(Charles F. Kettering)は,米陸軍用に,Kettering Aerial Torpedo(通称,ケタリング・バグ(Kettering Bug)の,初飛行試験を実施しました[YouTube 1:24].
しかし,第一次世界大戦の終了と共に,米国におけるドローン開発は停滞してしまいました.

図 Curtiss-Sperry Flying Bomb, 1918
1924年9月15日,アメリカ海軍研究所が開発したフェリックストウ F5L(アメリカのCurtiss H-12をベースに,英国フェリックストウ海軍工廠が開発したF.5の,更にアメリカでの量産用に改設計された機体)により,世界で初めての完全な無線遠隔操縦による離着陸(水上機なので離着水)を含む飛行に成功しました.しかし,1925年12月11日に失敗した後,米国のUAV研究は10年程停滞しました.
8.英国で航空標的(Aerial Target)誕生
英国では,南北戦争(American Civil War)において,北軍気球司令部(Union Army Balloon Corps)による「軍事諜報活動(Military Intelligence)=観測気球(Observation Balloon)+弾着観測(Artillery Observer)」を観戦した王立工兵隊将校の1862年の進言で,1878年に気球学校(School of Ballooning,〜1911)が設立され,これが王立航空工廠(Royal Aircraft Factory, RAF,1911〜1918),王立航空機関(Royal Aircraft Establishment, RAE,1918〜)へと発展して行きました.
なお,この頃は,まだ「ドローン」「ターゲットドローン(Target Drone)」「Unmanned Aerial Vehiclle(UAV)」等の呼称はありませんでした.
そして,第一次世界大戦(World War I,1914-1918年)における,飛行船ツェッペリン号(Airship Zeppelin)を用いたドイツの英国爆撃(German bombing of Britain)[書籍][HP1][HP2]に対抗する為に,1914年には,RAFで研究が開始されました.
英国における航空標的では,「電波誘導システムの父(Father of Radio Guidance Systems)」,或は,「遠隔操縦機の父(Father of Remotely Piloted Vehicles)」と呼ばれるアーチボルド・ロウ(Archibald Low)のRCシステムが使用されました.彼の特許は1923年迄,非公開でした.その初期の例が,RAFにおいてHenry Follandが設計した「Ruston, Proctor製AT(1916)」や,Sopwith Sparrowの原型となったSopwith社の「Aerial Target(1916)」でした[HP].これらは,1917年型ATと呼ばれています.なお,この機種も「Sopwith Sparrow」と呼ばれました.

図.Ruston, Proctor Radio Controlled Target Aircraft, RAF O870

図.Sopwith Sparrow Aerial Target(1916)

図.Unmanned Aerial Target (mark II) , RAF-O1053
1917年3月21日に,RAFにおいてGeoffrey de Havillandが設計し,エアコー社(Aircraft Manufacturing Company)が製造したATが試験飛行しました.これは,前述,米国のHewitt-Sperry Automatic Airplane(1917年9月初飛行試験)に先駆ける事,半年であり,世界で最初に飛行に成功した無線UAVでした.なお,デハビランドは,歴史上唯一のアカデミー賞主演賞を受賞した兄弟姉妹として知られるオリヴィア・デ・ハヴィランドとジョーン・フォンテイン姉妹(この二人の女優は共に日本生まれでした)の従兄です.
但し,これらは,第一次世界大戦中には実用化には至っていません.
参)世界初の水上ターゲットドローン
1897年に建造された合衆国艦船(United States Ship,USS),戦艦アイオワ(USS Iowa, Battleship No. 4)は,1919年に「4号沿岸戦艦(Coast Battleship No. 4)」と改称され,初の無線操縦標的艦となり,1923年にパナマ湾で沈没しました.これが,人類初の水上ターゲットドローンと思われます.
第一次世界大戦後,1922年7月初旬,RAE 1921 Target Aircraft/Missileの試験が開始されました. 1925年3月2日に実施された10回目の,そして最終の試験で,39分間の飛行を達成しました.
1925年,この後継として,小型化/重量化/高速化した自動操縦対艦誘導ミサイルLarynxの開発が,に開始されました.初号機は,1927年7月20日に,S級駆逐艦 HMS Strongholdのカタパルトから射出されましたが,直ぐにブリストル海峡に墜落しました.しかし,三番機は,同年10月15日に,112マイル飛行後,ターゲットから5マイル外れた場所に着弾しました[HP1][HP2].

図.RAE Larynx No. 3 on Catapult aboard HMS Stronghold
9.ドローンの起源,フェアリークイーン登場
1931年,RAEは, Fairey Aviation Company(1915年にCharles Richard Faireyにより設立)のFairey IIIのバージョンFであるFairey III Fを,対空射撃訓練用ATとして無線制御に改造しました.そして,1932年の1月,4月にHMS Variantから射出された1番機,2番機は失敗に終わったものの,1932年9月14日に射出された三番機は9分間飛行しました.1933年,これに「フェアリークイーン(Fairey Queen)」の愛称が与えられました.Fairey(個人名/会社名)とFairy(妖精)とが同音である事から,イングランドの詩人エドマンド・スペンサー(Edmund Spenser)の長篇叙事詩「妖精の女王(The Faerie Queene)」に因んで「Fairey Queen」と名付けられたものと思われます.そのせいか,「Fairy Queen」と言う綴りを使用している例も多く見られます(「Fairley」と言う綴りも散見されます).
この後で分かる様に,この「フェアリークイーン(named Fairey Queen aboard HMS Valiant)」こそが,「Drone」と言う呼称の起源と言って良いでしょう.

図.Fairey Queen on Catapult aboard HMS Variant(1932)
10.クイーンビー登場
前述のGeoffrey de Havillandはエアコーの技術/設計主任だったのですが,エアコーが経営危機に陥った時,1925年にデ・ハビランド・エアクラフト(de Havilland Aircraft Company)を設立して,エアコーDHシリーズの生産を受け継ぎました.そして,DH.51の小型版として,民間機DH.60 モス(DH.60 Moth)を1920年に飛行させました.Cirrusエンジンを搭載したものをCirrus Moth,Genetエンジンを搭載したものをGenet Moth,Gipsyエンジンを搭載したものをGipsy Moth等と呼んでいます.このDH.60を,構造強化/新主翼採用/軽武装搭載とした軍用練習機が,DH.60T(Moth Trainer)です.これが後に,DH.82 タイガーモス(DH.82 Tiger Moth)と呼ばれる様になりました.
このDH.82 Tiger Mothに,誘導用無線電波受信機とサーボユニットを搭載して,無人機としたものが,DH.82クイーンビー(DH.82 Queen Bee)で,1935年に初飛行しました.

図.クイーンビーを視察するチャーチル(1941/6/6)
参)「Queen Bee」という名称
この名称は,①「Fairey Queen」に敬意を表して「Queen」を使用し,②「Moth」が翅を持つ昆虫(内翅類/完全変態亜節)として選択された「飛ぶ昆虫」の名称にすると言う方針で考案されたものと思われます.条件①②を満足させる為には,社会性/真社会性を示す社会性昆虫の代表である「ハナバチ(Bee)」「カリバチ(Wasp)」「アリ(Ant)」の3つであり,最もポピュラーな「ハナバチ」が選択された結果です.なお,厳密に言えば,アリも膜翅目なので翅がありますが,飛行機の愛称としてはイメージしにくいでしょう.
実際,Queen Beeの代替機として,1937年6月11日に初飛行したターゲットドローンAirspeed AS.30の愛称は「クイーン・ワスプ(Queen Wasp)」です.つまり,呼称については「Bee→Drone→Wasp」と言う歴史があると言う事です.
参)「ブンブン言う」
ところで,「ブンブン言うからBee/Droneの名称が付いた」と言う説があります.しかし,当時の飛行機は全てプロペラであり,全ての航空機が「ブンブン言う」ので,これは「(Queen)Bee」の愛称の理由としては非常に弱いと言わざるを得ません.
一方,「ブンブン言う」昆虫の代表は,その名称そのものが「ブンブン言う=Buzz音を発する=Bumble」を含む「マルハナバチ(Bumblebee)」です.よって,「ブンブン言う」事を理由にするとすれば,「Queen Bumblebee」或は単に「Bumble Bee」となっていたでしょう.
更には,上述の「Bee→Drone→Wasp」の流れも勘案すれば,「ブンブン言うからBee/Droneの名称が付いた」と言うのは俗説です.
なお「Bumble Bee」と言う名称の航空機は実在します.Robert H. Starrが1979年から開発を開始し1984年に初飛行させた,当時の世界最小機「Bumble Bee」です.その後継機Bumble Bee IIは現在でも世界最小機となっています.
11.いよいよドローン登場
1935年,当時,米海軍作戦部長だったWilliam H. Standley提督は,第二次ロンドン海軍軍縮会議に出席する為,英国に滞在した際,Queen Beeのデモを見学し,その重要性に気付きました.1936年初頭に,帰国後,彼は航空局長Ernest J. King少将と議論し,無人航空機の重要性を確認し,その9箇条を作成しました.
1936年7月20日,King少将は,Delmer S. Fahrney少佐を無線制御機の担当責任者に任命しました.そして,Fahrney少佐は「Queen Bee(女王蜂)」に敬意を表して,自分達が開発する無人航空機のコードネームを「Drone(雄蜂)」と言う術語を当てました[HP1] [HP2] [HP3][HP4][HP5]{HP6][HP7][HP8].即ち,このFahrney少佐こそが「Drone」と言う呼称の生みの親です.今では,Fahrney少佐は「誘導ミサイルの父(Father of Guided Missiles)」として知られています.
さて,1936年,Fahrney少佐は,Stearman-Hammond Y-1Sを,コード番号JH-1として無線操縦機の開発を開始しました.無人無線操縦飛行試験が,1937年11月15日から開始され,1937年12月23日に全ての過程が成功しました.これは,離着陸〜高度200フィート以下では地上の制御車から操縦し,高度200フィート以上では管制機Great Lakes TG-2から操縦する,と言う形態でした.その後,Curtiss Fledglingのうち生き残ったN2C-2を,Target Droneに改造し,これも管制機Great Lakes TG-2から操縦しました(下図).
1938年9月14日,無線制御を使って,これも無線操縦である標的艦ユタ (AG-16) に突撃させました.ユタから対空砲撃が行なわれましたが,僅か2機を撃墜出来ただけで,大半のN2C-2は戻って来ました.結果として,対空砲火を有効に機能させるには(敵機を撃ち落とすには)どうすれば良いかについての示唆を得る事に繋がりました.そして,Claude C. Bloch提督は「この様な経験を実戦ではなく,練習として行なえた事は幸運だった」と述べています.なお,これは世界初の誘導ミサイルと見做されています.
Fahrney少佐は,TVシステムとレーダー高度計を使用して操縦できるものに改良する「Project Fox」を開始しました.1941 年 2 月 17 日迄に,TVシステムによる誘導は成功しました.このTVシステムを搭載した攻撃型ドローンを「アサルト・ドローン(Assault Drone)」 と呼びました.1942年4月9日,無人無線となったアサルトドローンTG-2は魚雷を抱えて突撃し,魚雷を放ちました.これは,世界最初の地対地誘導ミサイルとなりました.やがて,有名なアサルトドローンTDR-1が誕生します[YouTube 2:39].
12.ラジオプレーン
レジナルド・デニー(Reginald Denny)は,1899年デビューの英国の有名な俳優でした.第一次対戦中,英陸軍航空隊(Royal Flying Corps,RFC)でパイロットを務めたのち,米国に移住しハリウッド俳優となりました.
1934年,レジナルド・デニー(Reginald Denny)は,Robert Loraineと共に,Reginald Denny Industriesを設立し,ラジコン飛行機の開発を開始しました.1938年2月21日,米陸軍航空部隊を相手に,初期モデル「Radio Plane One, RP-1」のデモを行ないましたが上手く行きませんでした.しかし,軍の要求を満たした暁には,3機を購入すると言う約束を陸軍から取り付け,RP-2,RP-3と開発を続けました.
1939年の11月,RP-4の試作機により,米陸軍から53機を受注しました.このRP-4は,Walter Righterが設立したWalter Hammond Righterの工場で製作しされたツインローターエンジン「サイドワインダー」を搭載し,「ジョイスティック(Joystick)」による操縦が採用されました.これにより,アメリカ陸軍航空軍(United States Army Air Forces,USAAF)の援助を取り付けました.なお,このRP-4は米陸軍では「OQ-1」と呼称されました.この「Q」は米軍において「無人機」を意味するコード番号で,元々は「A Series」だったものが,OQがサブスケールドローンに,PQがフルスケールドローンに与えられる様になりました.その後には,(X)BQ-1,(X)BQ-2[HP],制御する側のドローンには,YCQ-1A(Fletcher FBT-2,恐らくcontrolのC)等があります.現在でも,「RQ-1プレデター」「MQ-9リーパー」等の様に使用されています.
1940年,デニーはRadioplane Companyを設立し,RP-4/OQ-1の生産を開始しました.

図.RP-4 / OQ-1用「サイドワインダー」を手に持つウォルター・ライター
1941年6月,更に改良され,二重反転プロペラとなったRP-5A[YouTube 1:02]の出荷が開始されました.このRP-5Aは,米陸軍では「OQ-2A」,米海軍では,前述のFahrney少佐による呼称「Drone」を踏襲して「Target Drone Denny One(TDD-1)」と呼称されました.OQ-2A/TDD-1は,USAAFとUSNの為に,1万5千機ほどが生産されました.
13.ドローンを組み立てるNorma Jeane Dougherty
最後に,ドローンに関係した有名な,しかし一部誤解されているエピソードを紹介しましょう.
1944年夏,俳優であったデニーの友人で,米軍第1映画部隊(First Motion Picture Unit)の指揮官だった俳優ロナルド・レーガン(Ronald Reagan,勿論,後の第40代米大統領)大尉は,写真家として訓練を受けたDavid Conover一等兵に,Radioplane Companyに行って,陸軍週刊誌ヤンク(YANK)用に,Rosie the Riveter(軍に協力して働く女性達)の士気を高める為の写真を撮る様に命じました.
1944年6月26日,コノバー一等兵はRadioplane Companyに向かいました.そこで,OQ-3/TDD-2を組み立てている一人の飛び切り魅力的な女性Norma Jeane Doughertyが,彼の目を惹き付けました.彼は,彼女をモデルとして,何枚かの写真を撮影しました(下図).その後,コノバーは写真を編集部へ送付しましたが,それは編集部には届かず失われてしまいました.結果として,掲載予定であった1944年12月22日号"Women in Industry"の記事は,Norma Jeaneの写真無しで掲載されました.現在残されている数枚の,この時のNorma Jeaneの写真は,コノバーの元に残っていたものです.


図.OQ-3を組み立ている(と言うポーズの)ノーマ・ジーン・ドハティ
参)ノーマ・ジーン
1944年6月26日の撮影の時,ノーマは映画スターになりたいとコノバーに相談しました.コノバーは,まずはモデルになる様,助言しました.1945年1月に工場を辞め,コノバーはノーマを,モデル事務所ブルー・ブック・モデル・エージェンシーの経営者Emmeline Snivelyに紹介し,8月に契約しました.Snivelyは彼女を「next door type」と評していました[YouTube 51-].ノーマは,ここでブルネットの巻き毛を,ブロンドのストレートに変更したのでした[YouTube 2:19-].
1946年6月に,俳優事務所と契約し,パラマウント映画の面接に落ちた後,1946年8月26日に,20世紀フォックスとの6ヶ月の契約が成立します.この時,ブロードウェイミュージカルスターMarilyn Millerと,母親の旧姓Gladys Pearl Monroeを組み合わせて,女優「マリリン・モンロー(Marilyn Monroe)」が誕生しました.ところが,1947年8月,20世紀フォックスは契約更新をしませんでした.その後,暫く下積み生活が続きます.彼女がブレークしたのは,1950年になってからで,同年12月に,再び,20世紀フォックスとの契約を勝ち取りました.
いくつかの情報源では,写真がYANKに掲載された事が切掛けでノーマがハリウッド入りしたかの様に誤った説明が散見されます.YANKに写真は掲載されませんでしたし,それによりノーマが評判になった事もありません.




図.1945年8月3日号(これもフェイクの年巻号です)
左はフェイク,右は実際のYANK(フェイク画像ではNoが故意に0になっています)
|





