風車とは?
風の持つエネルギーを回転する羽根を介して動力に変える原動機を風車(風力タービンとも呼ばれます)といい、 一般には増速機を介して発電機に連結され電気を作ります。
風車は最も古いターボ機械の1つで、蒸気機関が発明されるまで水車と共に、動力機関として使われてきました。 最近では、環境に易しい再生可能エネルギーとして、世界中で研究開発および導入が進んでいます。 風車には、軸が水平か垂直かで水平軸風車と垂直軸風車にわけられます。 通常よく目にするプロペラ形風車やオランダ形風車などは水平軸風車(図1)で、ダリウス形風車やサボニウス形風車、 ジャイロミル形風車などは垂直軸風車(図2)です。
また、風車翼が利用する流体力の成分によって、揚力形風車と抗力形風車に分けられます。 流れの中に置かれた物体には力が働きますが、その力を流れの方向の成分と流れと直角方向の成分に分解したとき、 流れ方向の力を抗力、直角方向の力を揚力と呼びます。 プロペラ形やダリウス形は揚力形風車で、サボニウス形などのような抗力形風車にくらべて、発生するトルクは小さいですが、 エネルギー変換効率は一般に高く、発電に適した高回転・低トルクの風車といえます。 一方抗力形風車は、ポンプなどの機械駆動に適した低回転・高トルクの風車といえます。
風車は最も古いターボ機械の1つで、蒸気機関が発明されるまで水車と共に、動力機関として使われてきました。 最近では、環境に易しい再生可能エネルギーとして、世界中で研究開発および導入が進んでいます。 風車には、軸が水平か垂直かで水平軸風車と垂直軸風車にわけられます。 通常よく目にするプロペラ形風車やオランダ形風車などは水平軸風車(図1)で、ダリウス形風車やサボニウス形風車、 ジャイロミル形風車などは垂直軸風車(図2)です。
また、風車翼が利用する流体力の成分によって、揚力形風車と抗力形風車に分けられます。 流れの中に置かれた物体には力が働きますが、その力を流れの方向の成分と流れと直角方向の成分に分解したとき、 流れ方向の力を抗力、直角方向の力を揚力と呼びます。 プロペラ形やダリウス形は揚力形風車で、サボニウス形などのような抗力形風車にくらべて、発生するトルクは小さいですが、 エネルギー変換効率は一般に高く、発電に適した高回転・低トルクの風車といえます。 一方抗力形風車は、ポンプなどの機械駆動に適した低回転・高トルクの風車といえます。

図1 洋上風車(プロペラ形風車)

図2 ダリウス風車
(九大・松宮教授提供)
(九大・松宮教授提供)
二乗三乗の法則に対する風車の挑戦
自然界には二乗三乗則と呼ばれる法則があります。動物のサイズ(長さL)を大きくしていきますと、面積SはL2に、 体積VはL3に比例しますので体重WもL3に比例します。すなわち、長さを2倍にすると面積は2乗の4倍、体積は3乗の8倍、 重さも8倍になります。したがって、動物の体重を支える部分、例えば脚には、単位面積当たりにかかる力 (応力といい、重さ/面積で計算します)は2倍に増えます。動物が自分の体重を支える骨格の割合は表1のようになり、 二乗三乗則にそって動物の骨格が決まることが端的に示されています。大きい動物と小さい動物を比較すると、 前者は面積に対する重さの割合が大きく、荷重を支える骨格の割合が多くなっています。
これは面積と重さの二乗三乗則ですが、もう一つの二乗三乗則があります。恒温動物では体の表 面から熱が逃げると仮定しますと標準代謝量PはP∝L2であり、重さW∝L3ですから、同じ代謝量に対する 体重はW/P∝Lで、大きくなるにしたがって標準代謝量当たりの体重が大きくなります。 P、Wの式からLを消去しますとP∝W2/3となります。この式は計算からですが、実際にはP∝W3/4と言われております(本川達雄著 ゾウの時間ネズミの時間)。べき乗の値が多少違っていますが、動物が大きくなると標準代謝量当たりの体重が大きくなるという傾向は変わらないです。
図3に示すような風車の場合、上と同じようなことが言えます。こちらの 方は生物的要因が入りませんので、材料や形状を変えず、幾何学的相似に保ったまま大きさを変化させますと、 厳密に上の2つの二乗三乗則が成立します。風車では、重力のほかに羽根の回転によって遠心力がかかりますが、 風車を大きくするとき、外周速度を同じにして回転数を下げる設計をしますので、羽根の根元にかかる遠心応力は同じになります。 ですから自重の影響だけを考えますと、Pを風車の出力、Wを風車の重さ、S1をタワーの横断面の面積に選びますと、W/P∝LおよびW/S1∝Lが成立します。
言い換えますと、風車を大きくすると、風車の自重と翼の自重による曲げモーメントはそれぞれそれを支える面積に比して大きくなり、 自重が出力に比して大きくなります。とくに、自重が大きくなることは、出力当たり材料費が上がることと同じであり、 風車の大型化は、経済的に成立しなくなります。一般に材料の大型化には、寸法効果と呼ぶ現象があります。 これは、大きくなるとそれだけ欠陥数が増え、材料の信頼性が落ちるというもので、このため材料の品質管理が重要になります。
しかし、良質な風が吹く場所は限られていますので、1箇所で大きな電力を得る価値が高いため、風車の大型化が進んでいるのです。 すなわち、風車の大型化はこの2乗3乗則を破る挑戦でもあるといえます。 軽量化を計ったり、形状を変えたりして、1990年代は300~500kW、2000年代は1~3MW(1MW=103kW)が商用化されており、 現在は4~5MWの開発が行われています。なお風車の出力Eは、風の速度をv、流量をQ、空気の密度をp、受風面積(風車翼が回転する面積) をS2 としますと、E=(1/2)ρQv2=(1/2)ρv3S2となり、風の速度の三乗に比例します。
これは面積と重さの二乗三乗則ですが、もう一つの二乗三乗則があります。恒温動物では体の表 面から熱が逃げると仮定しますと標準代謝量PはP∝L2であり、重さW∝L3ですから、同じ代謝量に対する 体重はW/P∝Lで、大きくなるにしたがって標準代謝量当たりの体重が大きくなります。 P、Wの式からLを消去しますとP∝W2/3となります。この式は計算からですが、実際にはP∝W3/4と言われております(本川達雄著 ゾウの時間ネズミの時間)。べき乗の値が多少違っていますが、動物が大きくなると標準代謝量当たりの体重が大きくなるという傾向は変わらないです。
図3に示すような風車の場合、上と同じようなことが言えます。こちらの 方は生物的要因が入りませんので、材料や形状を変えず、幾何学的相似に保ったまま大きさを変化させますと、 厳密に上の2つの二乗三乗則が成立します。風車では、重力のほかに羽根の回転によって遠心力がかかりますが、 風車を大きくするとき、外周速度を同じにして回転数を下げる設計をしますので、羽根の根元にかかる遠心応力は同じになります。 ですから自重の影響だけを考えますと、Pを風車の出力、Wを風車の重さ、S1をタワーの横断面の面積に選びますと、W/P∝LおよびW/S1∝Lが成立します。
言い換えますと、風車を大きくすると、風車の自重と翼の自重による曲げモーメントはそれぞれそれを支える面積に比して大きくなり、 自重が出力に比して大きくなります。とくに、自重が大きくなることは、出力当たり材料費が上がることと同じであり、 風車の大型化は、経済的に成立しなくなります。一般に材料の大型化には、寸法効果と呼ぶ現象があります。 これは、大きくなるとそれだけ欠陥数が増え、材料の信頼性が落ちるというもので、このため材料の品質管理が重要になります。
しかし、良質な風が吹く場所は限られていますので、1箇所で大きな電力を得る価値が高いため、風車の大型化が進んでいるのです。 すなわち、風車の大型化はこの2乗3乗則を破る挑戦でもあるといえます。 軽量化を計ったり、形状を変えたりして、1990年代は300~500kW、2000年代は1~3MW(1MW=103kW)が商用化されており、 現在は4~5MWの開発が行われています。なお風車の出力Eは、風の速度をv、流量をQ、空気の密度をp、受風面積(風車翼が回転する面積) をS2 としますと、E=(1/2)ρQv2=(1/2)ρv3S2となり、風の速度の三乗に比例します。
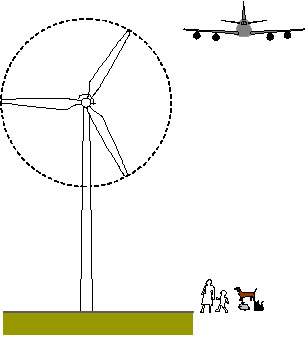
図3 風車
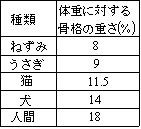
表1 哺乳類の骨格の割合
(出典 ヤイペレリマン「おもしろい力学」)
(出典 ヤイペレリマン「おもしろい力学」)
風車の翼は飛行機の翼とどう違うのでしょうか?
3MWのロータ外径は約90mで旅客機B747の全幅64.4mをはるかに上回っています。 風車が大きくなると、流れにおける力の関係、すなわち慣性力と粘性力(摩擦力)の割合が違ってきます。 この2つの力の比をレイノルズ数と呼び、フローパターンを決める重要なパラメータで、この値が変わると、翼のまわりの流動が違ってきます。
風車の羽根の周速度は先端部で速く、根元部では遅いので、先端部と根元部でも流れのレイノルズ数は約1桁も異なり、 両者の流れが違ってきます。また、羽根の遠心力は根元部が高いため、根元部の翼型が、図4に示しますように太った翼形になります。 このため、航空機では翼の先端で失速が起こりがちですが、風車では根元で失速が起こりがちで、流れの解析や実験を行い、 羽根の形状や翼型の選定が大変重要です。また羽根の設計によって騒音が違ってきます。
このように風車の空気力学的設計は大変重要で、風車を設計する場合、地形、気象条件、自然条件(鳥など)を十分検討して設計されます。 また強風に対する対策、落雷に対する破壊対策も大事です。
風車の羽根の周速度は先端部で速く、根元部では遅いので、先端部と根元部でも流れのレイノルズ数は約1桁も異なり、 両者の流れが違ってきます。また、羽根の遠心力は根元部が高いため、根元部の翼型が、図4に示しますように太った翼形になります。 このため、航空機では翼の先端で失速が起こりがちですが、風車では根元で失速が起こりがちで、流れの解析や実験を行い、 羽根の形状や翼型の選定が大変重要です。また羽根の設計によって騒音が違ってきます。
このように風車の空気力学的設計は大変重要で、風車を設計する場合、地形、気象条件、自然条件(鳥など)を十分検討して設計されます。 また強風に対する対策、落雷に対する破壊対策も大事です。
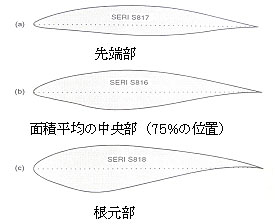
図4 米国再生可能エネルギー研究所の翼型
風車の用途
- 発電
- 回転エネルギーの熱変換(暖房、融雪、ハウス栽培など)
- ポンプの駆動(井戸水のくみ上げ、排水など)
- その他機械駆動(冷房、製粉など)
- 太陽電池発電との組み合わせ
|

